目次
マルコフ決定過程
4つの変数
マルコフ決定過程は、対象の状態S、状態の遷移P、行動A、状態の評価関数R、の4つのコンポーネントからなる確率事象に関する意思決定のモデルである。
- S 状態
- A 行動
- P 遷移
- R 評価 (報酬・利得であればRと書いて最大化を考え、費用や損失であればCと書いて最小化を考える)
状態Sの遷移Pには、次の2種類がある。
- 何も行動を取らず対象に介入しないことによる状態の遷移
- 何らかの行動Aを取り対象に介入することによる状態の遷移
ロボットなどの制御の問題では、何も行動を取らない場合には状態が遷移しない、とすることもある。以下では、遷移しないことも状態遷移の1つとして扱う。介入するか否か、また介入するならその内容は、介入後の状態の良し悪しを評価関数Rに基づいて評価して比較検討する
例えば、車で交差点に進入する状況を考える。そのままの車線を走り続ければ直進だが、駅に家族を迎えにきたのであれば、右折レーンに入って、右折の準備をするのが良い。その方が目標を果たすことに近付く。そこで、右折のウィンカーを点灯して右折レーンに入る、という操作を行う。これが介入である。
また、ロボットを格子状の盤の上に作った迷路の中に置き、ゴールGを目指させる状況を考える。ロボットは見通せる範囲の通路の形状しか認識できない。迷路の大きさも分からない。つまり、前後左右を向いたり、何歩が歩いたりしてみても、ゴールに近付いているかどうかを認識できない。状況を簡単にするために、ロボットは自分の前後左右が壁か通路かのみを認識できるとしよう。この時、どのような行動をとっていけば、ゴールに辿り着く確率が高まるだろうか。たとえ、ゴールの上に立たなければゴールに着いたことが分からないとしても、多くの試行を重ねることで、ゴールへ辿り着くための行動選択の指針を見出せることがある。
保全でも同様で、対象の状態を観測し、劣化の度合いに応じて、今、どの保全行動を取れば良いか、またもう少し遷移を見守るのが良いか、を将来に渡って運用し続けるために、余計な費用発生は避け、必要な費用発生は積極的に認めるように、保全行動を選択していく。
上の図はリンク先の企業の事業における劣化と保全の関係を表したものである。保全は社会を支える重要な技術であり、大きな市場を形成している。
行動の選択は、将来の状態の評価関数の予測を行い、最も評価が高くなるように行動を選択することが合理的である、という考え方に基づいて行う。将来の状態は、行動ごとに定められた遷移行列を繰り返し用いて行う。
これらのことを、マルコフ決定過程はモデル化していく。
方策と迷路の例
ロボットの状態を次のように考える。
| 番号 | 状態 |
| 1 | 正面に進める |
| 2 | 正面に進めない |
行動は次の3種類とする。
| 番号 | 状態 |
| 1 | 正面に進む |
| 2 | 右に90度回転する |
| 3 | 左に90度回転する |
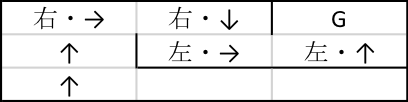
大きさ3×3の迷路が次のようになっているとする。
左下隅に、上向きにロボットを置く。人間であれば簡単に、ゴールまでたどり着くには、
| 時点 | 行動 |
| 1 | 1(前進) |
| 2 | 1(前進) |
| 3 | 2(右90度回転) |
| 4 | 1(前進) |
| 5 | 2(右90度回転) |
| 6 | 1(前進) |
| 7 | 3(左90度回転) |
| 8 | 1(前進) |
| 9 | 3(左90度回転) |
| 10 | 1(前進) |
という行動選択をすればいい、とたぶん分かる。
コンピュータ上であれば、最初の1ステップ目で
| 番号 | 状態 |
| 1 | 正面に進む |
| 2 | 右に90度回転する |
| 3 | 左に90度回転する |
を全て試して、ゴールにたどり着くかどうかを調べる。辿り着かなければ、それぞれのステップの次に
| 番号 | 状態 |
| 1 | 正面に進む |
| 2 | 右に90度回転する |
| 3 | 左に90度回転する |
を行う、3×3=9通りの行動の組み合わせを検討する。それでもだめなら、さらに9通りそれぞれの先に
| 番号 | 状態 |
| 1 | 正面に進む |
| 2 | 右に90度回転する |
| 3 | 左に90度回転する |
を行う、9×3=27通りの行動の組み合わせを検討する。これをゴールに到達するまで繰り返すのが、総当たり法である。
それに対して、マルコフ決定過程では状態が2つしかないことから、次のような状態とアクションの対応表を埋めようとする。
| 番号 | 状態 | 行動 |
| 1 | 正面に進める | |
| 2 | 正面に進めない |
この表を、方策policyという。 状態ごとにどのような選択をするかを、将来の評価関数を高めるように選んでいく。
状態の定め方が大事
実は、上の2状態では、常にゴールにたどり着ける解法はもとまらない。
| 番号 | 状態 | 行動 |
| 1 | 正面に進める | 進む |
| 2 | 正面に進めない | 右に回る |
上の方策を適用すると次のようになる。
| 手順 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
| 正面の状態 | 無 | 無 | 壁 | 無 | 壁 | 無 | 壁 | 壁 | 無 | … |
| 行動 | 前進 | 前進 | 右回転 | 前進 | 右回転 | 前進 | 右回転 | 右回転 | 前進 | … |
こうすると、途中でUターンしてしまい、永遠にスタート地点付近をさまようことになる。
一度、自分で確認してみてほしい。
| 番号 | 状態 | 行動 |
| 1 | 正面に進める | 進む |
| 2 | 正面に進めない | ランダムに右か左に回る |
これなら、運が良ければ、たどり着ける。
状態を次のように拡張してみる。
| 番号 | 状態 |
| 1 | 正面に進める |
| 2 | 正面が壁で、右手の壁がない |
| 3 | 正面が壁で、左手の壁がない |
| 4 | 正面が壁で、右手と左手の両方とも壁がない |
こうすると、例えば
| 番号 | 状態 | 行動 |
| 1 | 正面に進める | 進む |
| 2 | 正面が壁で、右手の壁がない | 右に90度回転する |
| 3 | 正面が壁で、左手の壁がない | 左に90度回転する |
| 4 | 正面が壁で、右手と左手の両方とも壁がない | 右に90度回転する |
という方策を学習できたとする。適用してみよう。
| 手順 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
| 正面の状態 | 無 | 無 | 壁 | 無 | 壁 | 無 | 壁 | 無 | 壁 | … |
| 左手の状態 | 壁 | 壁 | 壁 | 壁 | 壁 | 壁 | 無 | 無 | 無 | … |
| 右手の状態 | 無 | 壁 | 無 | 無 | 無 | 無 | 壁 | 壁 | 壁 | … |
| 行動 | 前進 | 前進 | 右回転 | 前進 | 右回転 | 前進 | 右回転 | 左回転 | 前進 | … |
これで有名な「右手づたいに壁を辿る」という迷路脱出のルールと等しくなる。 最後まで続けると、ゴールに辿り着く。
このように、マルコフ決定過程による問題解決には、適切な状態の表現が不可欠となる。
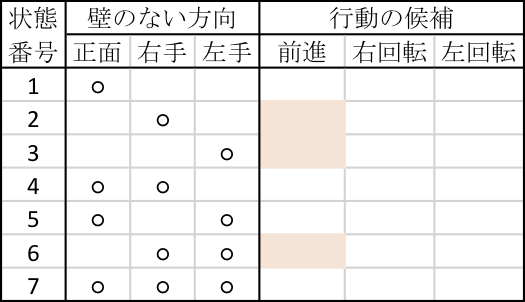
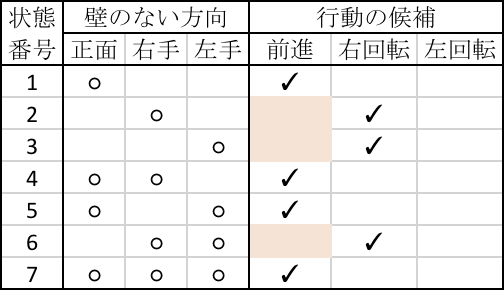
もう少し状態数を増やすと、次のような表ができる。
この表の右側にどの状況でどの行動を取るかを定めるのが、方策表である。 前に壁があると、進めないなど、選択できない行動のセルは塗りつぶしてある。
正前に壁がないのに前進しないと、いつまで経っても同じ場所に留まる方策ができあがってしまう。
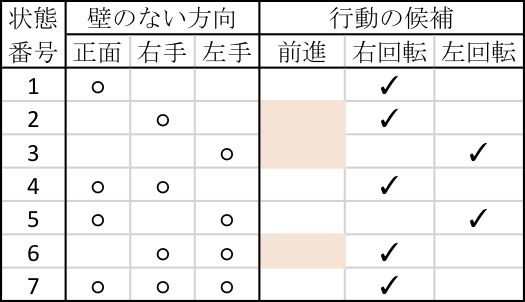
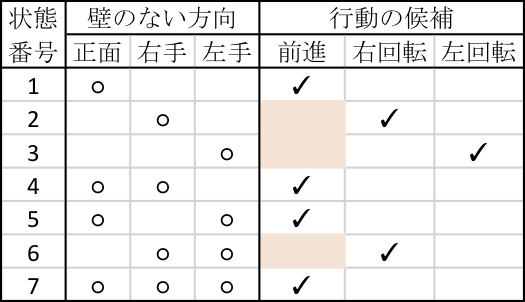
上の4状態での方策は、7状態でも次のようになる。
状態1,4,5,7は前進できるので前進、状態2,6,7は前進できないので右が空いていれば右、右が空いてなければ左に回転するので、同じ方策である。
方策の学習
上にも述べたがマルコフ決定過程では、状態と行動を結びつける表を方策という。 方策の最適化が、マルコフ決定過程を用いた対象のモデル化の目標である。
方策の候補をひとつ定める。
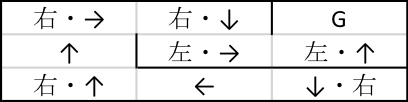
正前に壁が無ければ前進、壁があれば右回転、という方策を例にとる。 これを迷路の中に、ランダムな場所に、ランダムな向きにして置いたロボットに従わせる。 たとえば100ステップ内にゴールに辿り着けたら(100-到達ステップ数)点、辿り着けなければ0点として、何回も試行してみる。 例えば、上のこの例は0点である。
まったく到達できなければ、この方策をどこか一箇所、変更してみる。
そしてまたランダムに場所と向きを変えて置いて、迷路に挑戦させる試行を何度も繰り返して、この方策を評価する。上のもう1つの例は、100-10=90点を獲得する。
別の場所に下向きに置くと、100-14=86点を獲得する。
これを繰り返して、平均点をその方策の評価とする。
このように方策を比較して、良い方策を得るように探索をしていくのが、マルコフ決定過程の基本的な考え方である。1980年代から2000年代までは、ボードゲームのコンピュータのプレイヤーを作るのに、マルコフ決定過程の考え方がよく用いられていた。どのようなボードゲームにも、神の手と呼ばれる、誰でもその手順に従えば勝てる、という方策は存在せず、相手の手に合わせて状況を評価し、最善の手を打っていくことになる。ゲームでは、状況の数が膨大になり、取り得る行動もたくさんあるため、すべての行動の順列を比較検討すると、組み合わせ爆発が生じる。その爆発した組み合わせを、アドホックに刈り込んで、必要な組み合わせだけを比較するようにして、計算量を軽減する工夫が行われていた。
強化学習
上ででてきたQという関数を、様々な状態の対象に様々な行動を適用して、その結果から試行錯誤を繰り返すことで学習し、その下で最適な行動を選択していく。必要に応じて、アクションごとの状態推移も学習する。
https://gym.openai.com/envs/MountainCarContinuous-v0/
強化学習の話は、この原稿のスコープを大きく超えるので、別の機会に譲る。
マルコフ決定過程における方策の学習
マルコフ性の活用と状態遷移行列の活用
保全を施さない場合のシステムの劣化が、次の図で表されるマルコフ連鎖に従うとする。
これを行列で表すと、次のようになる。
| P[1→1]=9/10 | P[1→2]=1/10 | P[1→3]=0 |
| P[2→1]=0 | P[2→2]=9/10 | P[2→3]=1/10 |
| P[3→1]=0 | P[3→2]=0 | P[3→3]=1 |
選択した行動の実施によって生じる費用も次のように与える。
| 稼働 | 修理 | 取替 | |
| 1 | 0 | 10 | 150 |
| 2 | 0 | 50 | 150 |
| 3 | 2000 | 250 | 150 |
当初の状態が1だったとする。また、各状態の総期待費用が次の表で与えられているとする。
| 状態 | 1 | 2 | 3 |
| 費用V | 1 | 5 | 10 |
このとき、現時点で行動aを選択する時の1時点先の費用は次のように予測できる。
| 行動 | 稼働 | 修理 | 取替 | 最小値 | ||
| 1 | 0+0.9×1+0.1×5 | 10+0 | 150+0 | 1.4 | ||
| 2 | 0+0.9×5+0.1×2000 | 50+0 | 150+0 | 50 | ||
| 3 | 0+2000 | 250+0 | 150+0 | 150 | ||
この計算は例えば、現在の状態が2とする。何も介入しなければ、現時点では費用発生はなし。そして確率0.9で状態2に留まる。その場合には費用5が発生する。また確率0.1で状態3に進む。その場合には費用2000が発生する。これらのことから、状態2において行動「稼働」を選択した場合の総期待費用は0+0.9×5+0.1×2000=204.5と予測できる。他の状態と行動についても、同様に計算する。
これで状態ごとの最適行動が、次の表のように定まる。
| 状態 | 1 | 2 | 3 |
| 最適行動 | 稼働 | 修理 | 取替 |
価値関数あるいは費用関数
マルコフ連鎖に基づいて推移する対象に、保全行動によって介入する場合には、最適な行動を選択するためには、将来に渡る費用を算出する関数Vの学習が不可欠となる。 そのためのアルゴリズムを2つ紹介する。
学習アルゴリズム
価値関数V(s)の学習には大きく、policy iterationとvalue iterationという2種類のアルゴリズムがある。 以下では状態sにあって、行動aによって状態s^\primeに遷移する確率を P[s\prime|s,\pi(s\prime)] と書く。 以前の書き方では P(a)[s→s^\prime]であった。
迷路など、状態の遷移や行動の実行可能性に状態や環境による制約が加わる時には、それも考慮する。
ベルマン更新
時点tに状態がsの状況を評価する関数をV_t(s)と書く。 また時点tで行動aをとったときに、次の時点t+1に取る状態をS'(s,a)とする。 S'(s,a)は、sとaに依って変わる確率分布F(s|s,a)に従う確率変数である。
現時点では、状態sと行動aに応じて、費用が生じる。これが確率変数の場合は(条件ごとに異なる)条件付き期待値E[C|s,a]、定数の場合は条件によって定まる費用C(s,a)となる。これと、次の時点の状態S'(s,a)によって定まる費用V(S')の期待値の和が、状態sで行動aを執った場合の総費用となる。
将来の費用を現在価値に換算するために、割引係数β=1/(1+r)をかけるなら、次のようになる。
そして時点tの行動aをQt(s,a)を最小にするように選ぶ。
この計算式をベルマン更新という。
ベルマン方程式
現在の最適な行動と、その行動の帰結として将来に渡って発生する費用の総額は、勿論、将来の費用に依存する。t=∞の時点の費用が分かっていれば、例えば V∞(s)≡0ならば、そこから1時点ずつ遡ってVtを計算していくことが考えられる。この計算が、tを小さくするにつれて、つまり過去に遡るにつれて、ある一定の関数に収束するなら、その関数は次の方程式を満たす。
これがベルマン方程式である。ベルマン更新の式との違いは関数Vの添え字の有無しかない。でもこの違いは、Vが遷移している状態か、定常状態かの違いでもある。
将来の費用関数をどのように算出するか、そして将来の状態をどのように予測するか、がマルコフ決定過程がうまく働くための鍵となる。
報酬の場合
マルコフ連鎖に基づく予測
ベルマン方程式は、現在の状態sに基づいて、行動aを選択する際に、将来に渡って発生する費用を算出することができる。マルコフ決定過程において最も重要な式である。 将来の費用の予測の部分は、推移にマルコフ連鎖を仮定すると、ベルマン更新の方は次のようになる。
これを反映させた、ベルマン更新は次の式で定まる。
ベルマン方程式のための将来の費用の予測も同様に計算できる。
これを反映させた、状態と行動ごとのQ(s,a)は次の式で定まる。
これで、状態毎に予測を含む費用Q(s,a)を次のような表にまとめることができる。
| Q | 1 | 2 | A | |
| 1 | E[C(s=1,a=1)]+E[V(a=1)[1→S]] | E[C(s=1,a=2)]+E[V(a=2)[1→S]] | E[C(s=1,a=A)]+E[V(a=A)[1→S]] | |
| 2 | E[C(s=2,a=1)]+E[V(a=1)[2→S]] | E[C(s=2,a=2)]+E[V(a=2)[2→S]] | E[C(s=2,a=A)]+E[V(a=A)[2→S]] | |
| N | E[C(s=N,a=1)]+E[V(a=1)[N→S]] | E[C(s=N,a=2)]+E[V(a=2)[N→S]] | E[C(s=N,a=A)]+E[V(a=A)[N→S]] |
これがQ(s,1)、Q(s,2)、…、Q(s,A)の最も小さい値に対応する行動を、状態sにおける最適な行動とする。 これを状態sごとに最小化するベルマン方程式は次の式になる。
方策反復
まず状態と行動の対応表を一つ定める。この表を方策(policy)といい、πで表す。 方策が与えられるとは、 s ごとに a を与える関数π(s)が定まっていることを意味する。 この方策πを適用すると、次のようなQ関数が得られる。
これを状態ごとに最小にする方策を求める。
これを新しい方策とする。
このように方策を更新していくのが、方策反復policy iterationである。 収束するまでこれを繰り返して、最適方策を得る。 日本語では方策反復法と呼ばれることもある。
価値反復
value iterationは、ベルマン更新をそのまま用いる。
最終時点のVをひとつ与える。次にベルマン更新
によって、時点を1つ戻す。毎時点、費用を最小にするように状態sごとに行動aを選ぶ。 この対応が方策π(s)になっているが、そのことは特に意識しない。 そしてVt(s)が収束した時点の方策π(s)を最適方策、またそのときの関数Vt(s)をV(s)とする。
まとめ
上の二つのアルゴリズムはどちらも関数V(s)を与える。 この関数を用いて、現時点で将来の推移を考慮しながら、最適な行動を選択する。
要検討課題
価値反復と方策反復では、得られる方策の解が同じでも、総期待割引き報酬もしくは費用Vの値が異なる。なぜか?
Rでマルコフ決定過程の計算を行う
markovchainはマルコフ連鎖(離散時間離散状態マルコフ過程)の遷移行列の推定や、マルコフ過程の性質の解析決定を行う。
mdptoolboxはマルコフ決定過程の最適方策の学習を行う。
この2つを組み合わせると、データから遷移行列を推定して、その遷移行列と評価関数に基づいてマルコフ決定過程に基づく最適方策の学習を行う、という一連の最適化プロセスを実装できる。
保全とマルコフ決定過程
保全の問題では、対象システムに何も保全行動という介入しなければ、システムは劣化していく。 ただしその状態の遷移は、現在の状態とマルコフ行列に記された条件付き分布に従う。 ゲームはプレイヤーが複数いるのが通例だが、保全の問題では対象であるシステムが打ってくる手はとても単純で、保全行動を実行しなければ劣化による状態遷移が発生する。保全行動を実行すれば、その結果として状態が回復するという状態遷移が発生する。